In the late 2000s, when i was a wee child, my parents brought me along to the big yard sale organized in the tiny town my grandparents lived in. One particular time, we came back with a set of electronic gizmos that included a marine radio set. That huge cube of metal, with a deployable 2-meter long antenna ^[1], and a big selector to pick between various AM bands labeled with lengths, CB, Maritime Frequencies, etc, also came with a booklet left there by the previous owner with tables of names of foreign radios, and, in a big grid, hour intervals. That radio set is probably collecting dust in a garage at the moment, but it gave me a couple dozen hours of fun for the price of several 9V batteries.

Radio Listening: An Introduction

For most of my life, my only exposure to radio was via the commercial FM stations my parents listened to throughout the day when i was a kid, and in the car. i had several ideas in my mind about these elusive "radio waves":

• radio waves are electromagnetic and you can't feel them but they're there, and line of sight is important, but they can also bounce, somewhat; kind of like visible light
• radio waves were how TV and phone and WiFi worked, and sometimes you could be in a spot where no signal could exist, and a meter next to there you'd have great reception
• radio was AM or FM, and those meant that the sound was transmitted differently, although i had no idea how exactly
• you could tune to a specific number to hear a different signal, and it worked
• Signals could only travel so far, and different antennas in different regions would emit the same station sometimes at different frequencies

In August 2024 i bought a SDR. It's not a particularly good one; the point was that i wanted to explore radio frequency listening, something that had always lingered in the back of my mind, and recently became a newfound topic of interest within the French internet thanks to a couple videos by a French creator and musician.

and thus, i fell down the RF rabbit hole. This is sort of an introduction of a series of posts that will come in the future. Those posts will be more digestible little bites of exploration on specific topics, as opposed to the first draft of a huge post i originally attempted on this topic. Things we should cover, in no particular order:

• Listening in on my local airport
• Losing my mind at French RF regulation
• Eaves-dropping on the neighborhood kids and the chilling experience of knowing all you broadcast can be listened to
• That time i cobbled together a little raspberry pi, my phone and my SDR to listen to what everyone was saying downtown
• France being a paranoid country so even firefighters use encrypted comms
• That one time i received an industrial sensor alert via POCSAG (pagers) and shit myself (conversely: that one time i received a message via POCSAG with an exact address and someone's cause of death)
• Listening to an american pastor talk from thousands of kilometers away with a puny little stick of metal
• Soldering a bicycle brake wire to make the stupidest antenna in existence
• Running across a parking lot with an antenna pointed at the night sky and yelling "COME BACK HERE YOU FUCKING INTERNATIONAL SPACE STATION MY TAXES PAY FOR YOU"

And much more.

Don't expect necessarily 100%-accurate information either. i am armed with a SDR, and a computer science engineering degree. i might try to get my telco friends to check over this, and i can always pray to the Balanis for guidance, but the science gets over my head when we reach the physical layer of a medium. You can help me improve this by sending an email if you want.

A Primer on Electromagnetic Frequencies and Their Propagation

Nonetheless, here is a primer on information that should be necessary to follow along, but digestible. This section might be updated as i add and correct information for further posts in the series. If you are a physicist or work in telco, plug your ears and close your eyes:

Electromagnetic wave propagate in space. The space around us is full of electricity, or, rather, with the potential of electricity hanging around. Analogous to that, the air around is is like a big space full of individual points of air that can be more or less compressed locally. Like mechanical waves, EM waves are created by a disturbance in the field through which they propagate. The disturbance changes the property of the space, or milieu. For air, a sudden push will locally compress air, which will then push against the air nearby, and so on. For EM waves, the change in electrical potential will propagate in space, creating a change in the field locally, which propagates. The key property of waves is that they are a propagating disturbance that keeps even after the source of the disturbance has ceased acting on the milieu. Examples of that for sound waves are: your voice, or thunder. The sound of thunder travels to you even as you've already seen the strike hit and fade away, and the light of stars extinct for millions of years is still in the process of reaching us.

When propagating, electromechanical waves diminish in intensity as they travel and hit matter. The exact way they dissipate and how much they can traverse before being fully imperceptible depends on other properties. For light, that travel happens at a speed that physicist will ask you to consider to be constant, because theories seem to uphold that (at least last time i did an optics lab in university). The milieu of propagation actually impacts propagation ever so slightly, creating effects such as rainbows and most diffraction.

So far i've mostly talked about light, because it is the most intuitive form of electromagnetic wave. However, they exist on a spectrum. Waves are typically described by the "shape" they have: the way they modify the property of the milieu as time goes on. That "shape" changes depending on the source of the disturbance and potentially the shape of objects around (which is why a piano sounds different from a guitar, or a trumpet). That shape may be very uniform, as in the field of propagation (air, or the electromagnetic field) changes at a constant rate and a constant period, in which case you have a "pure" signal at one frequency: the interval of time it takes to return to a state of the wave you have already seen (also called a period). If your period is 1/440th of a second long for sound, you hear a nice A note. For electromagnetic waves, if you have exactly 530000 billion periods in a second, you are seeing the color green. Because periods get ridiculously small, we use frequency, the number of periods per second, with the "Hertz" unit. The prior examples are usually expressed as 440Hz (A note) and 530 THz (Terahertz, or 1000 billion hertz).

For electromagnetic waves we also tend to talk about the wavelength of a signal. Because light travels at a constant speed, we can know precisely how far it will have gone during one period at a given frequency. That length, the length of a wave, is used to characterize a pure signal. Our 530 THz green has a wavelength of about 565 nanometres. It means that if you placed precise measurement tools every 565 nanometres for that specific wave of green, which could extremely accurately measure the modification of the electric field, you would see them all show the same value. They would keep the same value if you slid them all alongside the direction of propagation.

Frequencies start at 0 (which is not technically possible on an alternating signal like we are talking about so far). From 0 to about 10^10 Hertz (or 10GHz), we find radio waves. Those have a wave length varying from about as big as possible (in most practical uses, at most the size of a skyscraper), all the way to an insect. At 2.5GHz (12cm wavelength), you've got your microwave oven's frequency for bringing water to a boil, and old standards for WiFi. At around 5.1Ghz all the way to 5.7GHz (~5.5cm wavelength), you get your modern WiFi 5. In general, we will be concerned with what happens between a couple hundreds of kilohertz, and about 1.5GHz.

So far i have only talked about electromagnetic waves of a given pure frequency, meaning that if you could visually observe the wave, you would see a change in the electromagnetic field around you happening uniformly, with the field going "up" for half the period, then "down" for the rest of the period, following a sine pattern, which would repeat forever. In reality, things are messy. As mentioned, not everything is a pure signal of one frequency, in fact, it would be highly impractical. So we do better.

In the 1810s, a guy by the name of Jean-Baptiste Joseph Fourier (yes, he is french, sorry), was interested in modeling how heat propagates in materials (he helped launch a little field of physics called thermodynamics, nothing big). After settling in the french city of Grenoble, he worked at the theory and figured that heat propagates between two objects based on the difference in temperature they show. As part of his work on the matter, Fourier actually developed a nice property that we still use to this day: under certain circumstances, a seemingly chaotic function can be broken down into a (potentially infinite) sum of decreasingly big sine waves. For the less mathematically inclined, this means that if you take any form of wave in the right circumstances (and in physics we can assume those for any wave), we can break that seemingly chaotic variation of the field into a set of variations of one frequency with different proportions, or what i've been calling for now "pure signals", i.e. sine waves.

In space, when a piece of equipment puts out a disturbance of the EM field, it can be decomposed as modifications of precise frequencies through an operation called the Fourier transform, where we take the input signal and break it down into individual frequencies and how much they are being affected. When two signals collide in space, these base components add to each other. In some circumstances, this means that one signal will cancel out the other: if two signals of exactly the same pure frequency, but slightly shifted in time, collide, the sum of modifications to the propagation milieu will be null: there will be no signal. In sound, this is the technology behind active noise cancelling (where the headphones play an inverted recording of your environment's noise to subtract the noise from the signal your ears receive). In other circumstances, two signals can collide and amplify one another.

So, back to electromagnetic waves, we want to encode some sort of information into electromagnetic waves. Having Fourier transforms, which our computers and analog electronics can do reasonably well, is doable. In fact, electronics are actually really good, when given AC voltage at the right frequency, and with the correct components, at creating an alternating current that can have a precise frequency and intensity. If, by chance, that alternating current is going down through a piece of conductive material, the change in motion of the electricity through the wire will create a magnetic wave around the wire. If that change keeps repeating, the magnetic wave (which at that point will have also created changes in the electric field, meaning that the wave is both electronic and magnetic) will start alternating at exactly the frequency, or frequencies we want. This is, roughly, radio emission. The converse operation happens when a piece of metal is present and influenced by a change in its surrounding electromagnetic field, creating tiny changes in current in the wire, which can be picked up by precise components down the line, and interpreted as reception of an electromagnetic wave: that's reception, with an antenna.

To receive radio waves, i use a software defined radio, or SDR. Typical radios you will find are meant to be used on commercial bands, where voice is broadcast either via the (wideband) FM or AM modes. Your radio will shift some properties of its analog (or digital) components (a bit of resistance here, a bit of capacitance there), and suddenly it is attuned to changes at a particular frequency, and those nearby. In a software defined radio, my computer is the one telling the SDR what it needs to attune to. The SDR is made up of three important components: an antenna to pick up a signal (i actually plug it into the dongle, but that's irrelevant because it's necessary anyways), a decoder chip that interprets the incoming electrical noise as signals, and a tuner that changes parameters of the decoder chip to target a certain range of reception frequencies.

Encoding information into an electromagnetic signal usually follows one of two methods: amplitude modulation or frequency modulation. In reality, many others exist, but i will focus on voice for now, which, unless you are using a digital transmission system, uses of those two. Your voice, and whatever else music is mixed with it, is an analog signal that can typically vary up to about 20 KHz (the range the human ear can pick up). In order to encode the information, the emitter picks a frequency, called the carrier.

In amplitude modulation (AM), the analog signal is used to change the amplitude of the carrier. Imagine your nice sine wave, repeating at the frequency of the carrier that you've picked (e.g. 100 KHz), except the sine does not go up to 1 or -1 every time. The contour of the sine draws the shape of the much lower frequency signal that you want to express:

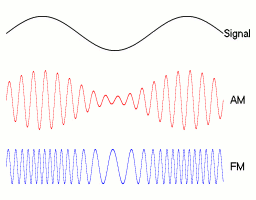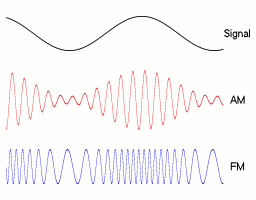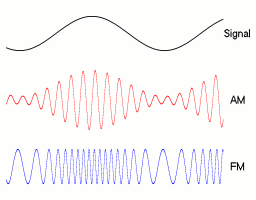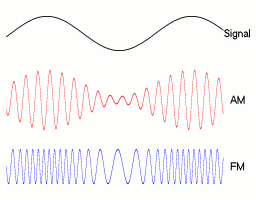
By Berserkerus - Own work, CC BY-SA 2.5, Link

In frequency modulation, you take the variation of the input signal to change the frequency of the carrier. That is, if your signal is a nice sine wave like shown above, your FM signal will alternately have a slightly higher frequency than its carrier, then a slightly lower frequency. The effect of this is that your signal, once processed to decompose it into its pure components via a Fourier transform, will exhibit a peak that oscillates around the frequency of the carrier. To simplify, AM draws the signal on the amplitude you measure, whereas FM draws the signal on the Fourier decomposition.

This is why you typically need to capture a range of frequencies around the carrier. Information is actually encoded in a given range of frequencies. Even for amplitude modulation, where we multiply the carrier and the signal, the resulting signal is actually a sum of sines that are around the frequency of the carrier. In fact, for the AM mode, the range that these frequencies can take is twice the range of frequencies of the input signal. For FM, it is the same as the input signal. That range of frequency that is listened to to demodulate your signal is called the bandwidth of the signal.

The typical way you will show the presence of electromagnetic waves and how they break down into individual frequencies is called a spectrogram, it will show the spectrum of frequencies that you are interested in. A very specific type of spectrogram is often used by radio software, is called the waterfall spectrogram. An example is shown below:

By Konung yaropolk - Own work, CC0, Link

In waterfall displays of a spectrum, a gradient of colors (here blue to dark red) encodes how intense the received frequency is, which is its amplitude. Recall that a signal diminishes in intensity, or amplitude, the weaker it gets.

Conclusion

So, this is about as much as i can cram into a single article, and about as much as i can explain before we get into other stuff that can be explained in another article. This section is absolutely getting updated at some point, but we'll see.

See you by the spectrum waterfall~

1. or at least it felt that long when i was like, 8. ↩